- 看前吐槽一下,hexo 的公式编码真麻烦,markdown 语法老是有问题
反馈控制系统的典型结构 3.3.1-3.3.2
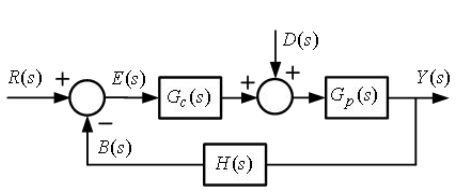
系统开环传递函数
系统开环传递函数定义为
$$G_L(s)=\frac{B(s)}{R(s)}=G_c(s)G_p(s)H(s)$$
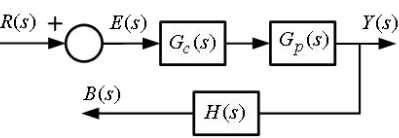
当 H(s) = 1 时,系统被称为单位反馈
闭环传递函数
参考输入 R(s)作用下的闭环传递函数
$$T_R(s)=\frac{Y(s)}{R(s)}=\frac{G_c(s)G_p(s)}{1+G_c(s)G_p(s)H(s)}=\frac{G_c(s)G_p(s)}{1+G_L(s)}$$
扰动输入 D (s)作用下的闭环传递函数
$$T_D(s)=\frac{Y(s)}{D(s)}=\frac{G_p(s)}{1+G_c(s)G_p(s)H(s)}=\frac{G_p(s)}{1+G_L(s)}$$
偏差传递函数
偏差 e (t)=给定输入信号 r (t)-主反馈信号 b (t)
参考输入 R(s)作用下的偏差传递函数
$$T_{RE}(s)=\frac{E(s)}{R(s)}=\frac{1}{1+G_{c}(s)G_{p}(s)H(s)}=\frac{1}{1+G_{L}(s)}$$
扰动输入 D (s)作用下的偏差传递函数
$$T_{DE}(s)=\frac{E(s)}{D(s)}=\frac{-G_p(s)H(s)}{1+G_c(s)G_p(s)H(s)}=\frac{-G_p(s)H(s)}{1+G_L(s)}$$
系统稳定性的初步认识
假设有界外部干扰使系统偏离平衡状态。若瞬间干扰消失后,系统最终能够回到平衡状态,则称该系统是稳定的。否则,称该系统不稳定
一般概念
定义 1: 零初始条件下,若系统在有界输入(参考输入或干扰输入) 的作用下,其输出响应也是有界的,则称系统是稳定的。 (也叫做,有界输入有界输出稳定, Bounded-Input Bounded-Output, BIBO 稳定)
BIBO 稳定最具代表性
稳定性的定义多种多样
定义 2:零初始条件下,若输入信号 $r(t)$ 在 $(0,\infty]$ 上满足 $|r(t)|\leq N$, 系统在其作用下的输出相应 $y(t)$ 满足 $|y(t)|\leq M$, 则称该系统是稳定的。其中 $N,M$ 均为常数。
闭环传递函数的极点与系统的稳定性
以线性定常连续系统为例:$Y(s) = G(s)R(s) \Rightarrow y(t) = \int_{0}^{+\infty} g(\tau)r(t-\tau)d\tau$
$\left|y(t)\right| = \left|\int_{0}^{+\infty} g(\tau)r(t-\tau)d\tau\right| \leq \int_{0}^{+\infty}\left|g(\tau)r(t-\tau)\right|d\tau \leq \int_{0}^{+\infty}\left|g(\tau)\right|\left|r(t-\tau)\right|d\tau \leq N\int_{0}^{+\infty}\left|g(\tau)\right|d\tau \leq M$
而 $\int _{0}^{+\infty }\vert g(\tau )\vert d\tau \leq \frac {M}{N}$ 意味着什么?
什么因素决定了传递函数的脉冲响应是收敛的?
闭环传递函数的极点与系统的稳定性
抛砖引玉,考虑系统: $$G(s)=\frac {N(s)}{\Delta (s)}=\frac {1}{(s+1)(s+2)(s^{2}+2s+2)}$$
$$=\frac {1}{s+1}+\frac {-2}{s+2}+\frac {-2+2j}{s+1+j}+\frac {-2-2j}{s+1-j}$$
那么反拉式变换$$L^{-1}{G(s)}=e^{-t}-2e^{-2t}+(-2+2j)e^{-(1+j)t}+(-2-2j)e^{-(1-j)t}$$
$$=e^{-t}-2e^{-2t}+(-2+2j)e^{-t}e^{-jt}+(-2-2j)e^{-t}e^{jt}$$
$$=e^{-t}-2e^{-2t}+4e^{-t}(\sin t-\cos t)$$
那么 G(s)有以下的形式
$$G(s)=\frac{N(s)}{\Delta(s)}=\frac{K_g\prod_{i=1}^m(s+z_i)}{\prod_{l=1}^{n_1}(s+p_l)\prod_{l=n_1+1}^{n_1+(n-n_1)/2}(s+\sigma_l-j\omega_l)(s+\sigma_l+j\omega_l)}$$那么 $L^{-1}{G(s)}=?$
包含$e^{-p_{l}t}$
$$L^{-1}{\sum _{l=1}^{k}\frac {b_{l}}{(s+p)^{l}}}$$包含 $e^{-pt},te^{-pt},$ $t^{2}e^{-pt},\cdots ,$ $t^{k-1}e^{-pt}$
$$L^{-1}\left\{\sum_{l=n_{1}+1}^{n_{1}+(n-n_{1})/2}\left(\frac{c_{l}}{s+\sigma_{l}-j\omega_{l}}+\frac{d_{l}}{s+\sigma_{l}+j\omega_{l}}\right)\right\}$$包含 $e^{-\sigma _{l}t}\cos \omega _{l}t,$ $e^{-\sigma _{l}t}\sin \omega _{l}t$
$e^{-p_{l}t},e^{-pt},te^{-pt},$ $t^{2}e^{-pt},\cdots ,$ $t^{k-1}e^{-pt},$ $e^{-\sigma _{l}t}\cos \omega _{l}t,$ $e^{-\sigma _{l}t}\sin \omega _{l}t$:应该看作模态!
线性定常连续系统有界输入有界输出稳定的充分必要条件
证明略,就是解得要负实部
稳定性分析 vs 稳定化设计
考虑某一个系统的稳定性
$G(s)=\frac {N(s)}{\Delta (s)}$
Δ(s)=0 的解是否均具有负实部——稳定性分析
① 是,稳定性分析结束
② 否,需要增加反馈控制器使得新的闭环系统稳定
对于传递函数是 $\frac {Y(s)}{R(s)}=\frac {G_{c}(s)G(s)}{1+G_{c}(s)G(s)}$
需要设计合适的 $G_{c}(s)$使得$1+G_{c}(s)G(s)=0$的解均具有负实部