自动控制原理第二章

Chris

2024-07-25

系统的微分方程

物理系统微分方程

[!note]
步骤

定义系统及其组成元件

确定必要的假设条件

利用系统自身的物理规律

利用各组成元件的原始方程和前面所确定的输入量、中间变量和输出量，消去中间变量，建立描述系统输入量与输出量之间关系的微分方程

若得到的是线性微分方程，通常将其列写为标准形式，即将与输出量和输入量有关的各项分别列写在等号左右两边**（左出右入），并且两边各导数项均按降幂排列**。若得到的是非线性微分方程，则需要对非线性微分方程进行线性化处理才能列写为线性微分方程的标准形式

线性叠加
例 p24
几阶系统看最高次导数
时间常数 $T_m=J_m R_a /\left(\beta_m R_a+C_e C_m\right)$
电压传递常数和转矩传递常数 $\frac{C_m}{\beta_m R_a+C_e C_m} u_a(t)-\frac{R_a}{\beta_m R_a+C_e C_m} M_c(t)$

微分方程的增量化和无因次化

增量化

微分方程变量各阶导数为 0，变化率 0，也称为静态数学模型，例如 t=0 系统处于稳定工作状态，又称为平衡状态，此时各变量可视为常量，则各阶导数均为零
初步认识：微分方程=稳态+瞬态
平衡状态方程，导数等于 0，解出当前 t0
非增量微分方程消去常数项后，各变量前添加 Δ

无因次化

考虑微分方程 $T_{m} \frac{d \omega( t )} {d t}+\omega( t )=K_{u} u_{a} ( t )-K_{M} M_{c} ( t )$
平衡位置： $\omega( t_{0} )=\omega_{0}, \ \ u_{a} ( t_{0} )=u_{a 0}, \ \ M_{c} ( t_{0} )=M_{c 0},$
满足 $\omega_{0}=K_{u} u_{a 0}-K_{M} M_{c 0}$
再令：

$$\overline{{{{\omega}}}} ( t ) \!=\! \frac{\omega( t )} {\omega_{0}}, \ \ \overline{{{{u}}}}_{a} ( t ) \!=\! \frac{u_{a} ( t )} {u_{a 0}}, \ \ \overline{{{{M}}}}_{c} ( t ) \!=\! \frac{M_{c} ( t )} {M_{c 0}} $$ $$T*{m} \frac{d \overline {{{{\omega}} }} ( t )} {d t}+\overline {{{{\omega}} }} ( t )=\frac{K*{u} u*{a 0}} {\omega*{0}} \overline {{{{u}} }}_{a} ( t )-\frac{K_{M} M*{c 0}} {\omega*{0}} \overline {{{{M}} }}\_{c} ( t )$$

时间还是绝对化描述
令 $\tau=t / T_{m}$
$T_{m}$ 为时间常数，作为标称$$\frac{d \overline{{{{\omega}}}} ( \tau T_{m} )} {d \tau}+\overline{{{{\omega}}}} ( \tau T_{m} ) \!=\! \frac{K_{u} u_{a 0}} {\omega_{0}} \overline{{{{u}}}}_{a} ( \tau T_{m} ) \!-\! \frac{K_{M} M_{c 0}} {\omega_{0}} \overline{{{{M}}}}_{c} ( \tau T_{m} ) \!$$

非线性方程线性化

在小范围内线性处理，且选择在平衡状态点进行增量化描述
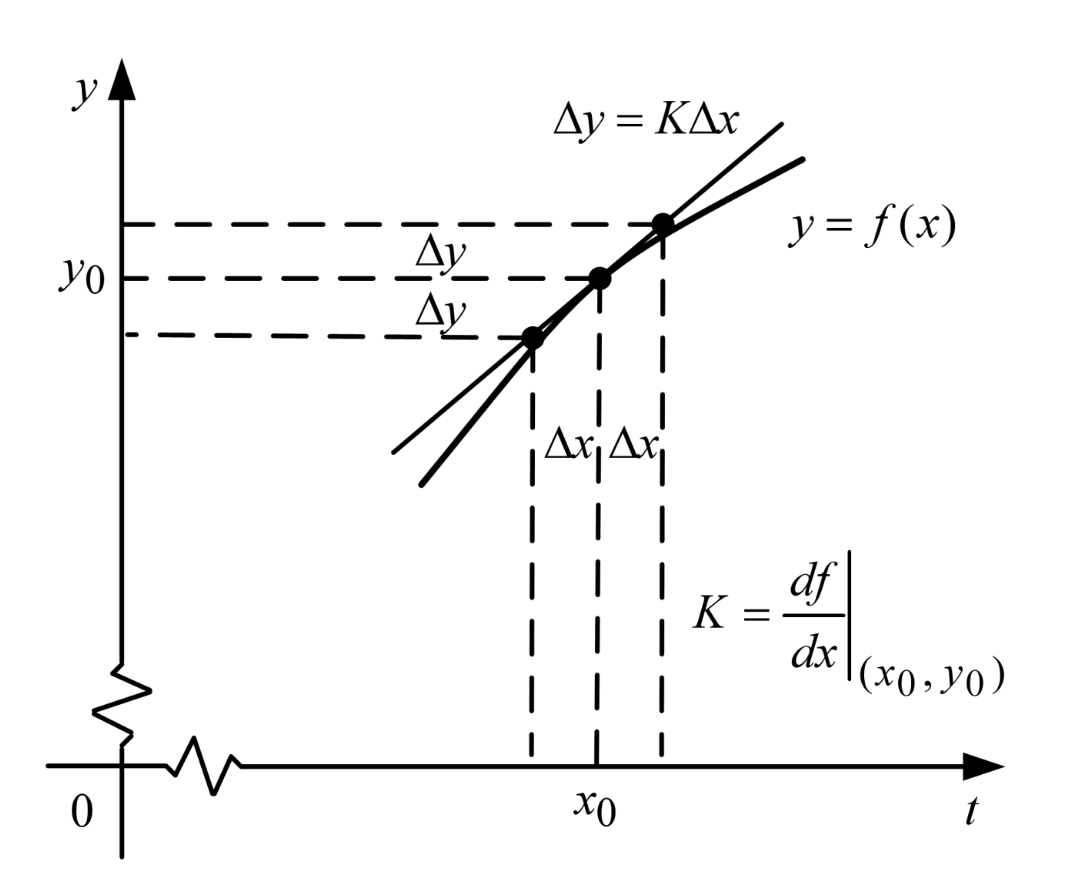
考虑高次，低次去掉偏导

$$\begin{aligned} {{y ( t )}} & {{} {{}=f ( x_{1} ( t ), x_{2} ( t ) )}} \\ {{}} & {{} {{} {}=f ( x_{1 0}, x_{2 0} )+\frac{\partial f ( x_{1}, x_{2} )} {\partial x_{1}} \Bigg|_{\stackrel{x_{i}=x_{i 0}} {x_{i}=x_{i 0}}} \frac{\Delta x_{1}} {1!}+\frac{\partial f ( x_{1}, x_{2} )} {\partial x_{2}} \Bigg|_{\stackrel{x_{i}=x_{i 0}} {x_{i}=x_{i 0}}} \frac{\Delta x_{2}} {1!}}} \\ \end{aligned} $$ $$+ \frac{\partial^{2} f ( x*{1}, x*{2} )} {\partial x*{1}^{2}} \Bigg|*{x*{1}=x*{i*{0}} \atop x*{2}=x*{i*{0}}} \frac{\big( \Delta x*{1} \big)^{2}} {2!}+\frac{\partial^{2} f ( x*{1}, x*{2} )} {\partial x*{2}^{2}} \Bigg|_{x_{1}=x*{i*{0}} \atop x*{2}=x*{i*{0}}} \frac{\big( \Delta x*{2} \big)^{2}} {2!}+\cdots $$

当增量 Δx1=x1-x10 Δx2=x2=x20 足够小，忽略高次方的项

$$\begin{array} {r} {{{\Delta y ( t )=y ( t )-y_{0}=f ( x_{1} ( t ), x_{2} ( t ) )-f ( x_{1 0}, x_{2 0} )}}} \\ {{{=\left. \frac{\partial f ( x_{1}, x_{2} )} {\partial x_{1}} \right|_{x_{1}=x_{0}} \Delta x_{1} ( t )+\left. \frac{\partial f ( x_{1}, x_{2} )} {\partial x_{2}} \right|_{x_{1}=x_{0}} \Delta x_{2} ( t )}}} \\ {{{=K_{1} \Delta x_{1} ( t )+K_{2} \Delta x_{2} ( t )}}} \\ \end{array} $$ $$其中K_{1}=\frac{\partial f ( x_{1}, x_{2} )} {\partial x_{1}} \Bigg|_{\stackrel{x_{1}=x_{1 0}} {x_{2}=x_{2 0}}} \;, \; \; \; K_{2}=\frac{\partial f ( x_{1}, x_{2} )} {\partial x_{2}} \Bigg|_{\stackrel{x_{1}=x_{1 0}} {x_{2}=x_{2 0}}} $$

传递函数

引入复数将时间域问题转化为复频率域问题来研究，将解微分方程问题简化为解代数问题

线性系统传递函数的概念和定义

传递函数=系统输出的拉氏变换/输入的拉氏变换
输入与输出之间的关系（固有特性）, 与输入的具体形式无关，都以相同的传递作用输出
标准线性系统的传递模型$$G ( s ) \!=\! \frac{Y ( s )} {U ( s )} \!=\! \frac{b_{m} s^{m}+b_{m-1} s^{m-1}+\cdots+b_{1} s+b_{0}} {a_{n} s^{n}+a_{n-1} s^{n-1}+\cdots+a_{1} s+a_{0}} $$
初始条件下有$$f ( 0 )=f^{\prime} ( 0 )=\cdots=f^{n-1} ( 0 )=0 \,, \ \ L \Biggl[ \frac{d^{n} f ( t )} {d t^{n}} \Biggr]=\Biggl( s^{n} F ( s ) \Biggr) $$
通过上式，下式两边拉氏变换

$$\begin{aligned} {{a_{n} {\frac{\mathrm{d}^{n} y ( t )} {\mathrm{d} t^{n}}}}} & {{} {{}+a_{n-1} {\frac{\mathrm{d}^{n-1} y ( t )} {\mathrm{d} t^{n-1}}}+\cdots+a_{1} {\frac{\mathrm{d} y ( t )} {\mathrm{d} t}}+a_{0} y ( t )}} \\ {{}} & {{} {{}=b_{m} {\frac{\mathrm{d}^{m} u ( t )} {\mathrm{d} t^{m}}}+b_{m-1} {\frac{\mathrm{d}^{m-1} u ( t )} {\mathrm{d} t^{m-1}}}+\cdots+b_{1} {\frac{\mathrm{d} u ( t )} {\mathrm{d} t}}+b_{0} u ( t )}} \\ \end{aligned} $$

有如下，化简最后得到标准的模型$$\begin{aligned} {{a_{n} s^{n} Y ( s )+}} & {{} {{} a_{n-1} s^{n-1} Y ( s )+\cdots+a_{1} s Y ( s )+a_{0} Y ( s )}} \\ {{}} & {{} {{} {}=b_{m} s^{m} U ( s )+b_{m-1} s^{m-1} U ( s )+\cdots+b_{1} s U ( s )+b_{0} U ( s )}} \\ \end{aligned} $$
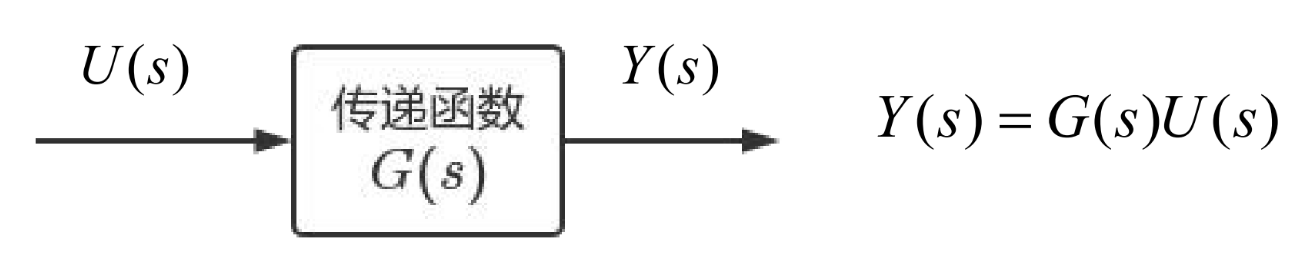
对于多个输入，分析时，将另外一个输入关闭

$$\Omega( s )=G_{1} ( s ) U_{a} ( s )+G_{2} ( s ) M_{c} ( s ) $$

[!note] 说明

传递函数是对线性定常微分方程求拉普拉斯变换得到的，因此，传递函数表达式中各项系数的值完全与微分方程中各导数项的系数相对应，取决于系统的结构和参数。

分母最高次 n，n 阶系统，n≥m，真有理函数

单入单出

传递函数常用表现形式

零、极点表示的形式$$G ( s )=\frac{b_{m}} {a_{n}} \times\frac{s^{m}+d_{m-1} s^{m-1}+\cdots+d_{1} s+d_{0}} {s^{n}+c_{n-1} s^{n-1}+\cdots+c_{1} s+c_{0}} = K_{g} \, \frac{( s+z_{1} ) ( s+z_{2} ) \cdots( s+z_{m} )} {( s+p_{1} ) ( s+p_{2} ) \cdots( s+p_{n} )}=K_{g} \, \frac{\prod_{i=1}^{m} ( s+z_{i} )} {\prod_{l=1}^{n} ( s+p_{l} )} $$
实数极点和共轭复数极点细化形式

不同极点种类性质不同$$G ( s )=\frac{K_{g}} {s^{\nu}} \times\frac{\prod_{i=1}^{m} ( s+z_{i} )} {\prod_{l=\nu+1}^{\nu+n_{i}} ( s+p_{l} ) \prod_{l=\nu+n_{i}+1}^{\nu+n_{i}+( s-\nu-n_{i} ) / 2} ( s^{2}+2 \zeta_{l} \omega_{l} s+\omega_{l}^{2} )} $$
$K_{g}=\frac{b_{m}} {a_{n}}$ ,称增益或传递系数
-z : 传递函数的零点，由 $G ( s )=0$ 求得，用“”表示;
$- p_{l}$ : 传递函数的极点，由 $G ( s )=\infty$ 求得，用“×”表示;
v：系统型数，决定稳态误差
共轭极点：与震荡有关

时间常数表示

$$G ( s )=\frac{b_{0}} {a_{0}} \times\frac{d_{m}^{\prime} s^{m}+d_{m-1}^{\prime} s^{m-1}+\cdots+d_{1}^{\prime} s+1} {c_{n}^{\prime} s^{n}+c_{n-1}^{\prime} s^{n-1}+\cdots+c_{1}^{\prime} s+1}=K \frac{( \tau_{1} s+1 ) ( \tau_{2}^{2} s^{2}+\tau_{2} \zeta s+1 ) \cdots( \tau_{i} s+1 )} {( T_{i} s+1 ) ( T_{2}^{2} s^{2}+T_{2} \zeta s+1 ) \cdots( T_{j} s+1 )} $$ $$G ( s )=\frac{K} {s^{\nu}} \times\frac{\prod*{i=1}^{m} \left( \tau*{i} s+1 \right)} {\prod*{l=\nu+1}^{\nu+n*{i}} ( T*{l} s+1 ) \prod*{l=\nu+n*{i}+1}^{\nu+n*{i}+( n-\nu-n*{i} ) / 2} ( T*{l}^{2} s^{2}+2 \xi*{l} T*{l} s+1 )} $$

$\tau_{i}, T_{i}$ : 时间常数
$K : K=G ( 0 ),$ 直流增益或静态放大系数

典型输入信号及其拉普拉斯变换

单位阶跃信号

$$1 ( t )=\begin{cases} {{{1,}}} & {{{t \geqslant0}}} \\ {{{0,}}} & {{{t < 0}}} \\ \end{cases}. $$ $$L {\bigl[} 1 ( t ) {\bigr]}={\frac{1} {s}} $$

单位斜坡函数

$$r ( t )=\left\{\begin{array} {c c} {{{t,}}} & {{{t \geqslant0}}} \\ {{{0,}}} & {{{t < 0}}} \\ \end{array} \right. $$ $$L \bigl[ r ( t ) \bigr]=\frac{1} {s^{2}} $$

单位抛物线
单位脉冲函数

$$\delta( t )=\operatorname* {l i m}_{\varepsilon\to0} \delta_{\varepsilon} ( t ) $$ $$\delta\_{\varepsilon} ( t )=\left\{\begin{aligned} {{{0}}} & {{{} {{},}}} & {{{{} {} {{} t < 0}}}} \\ {{{{}}}} & {{{} {{} {{} \frac{1} {\varepsilon}},}}} & {{{{} 0 \leq{}t \leq\varepsilon}}} \\ {{{{}}}} & {{{}}} \\ {{{{0},}}} & {{{{} {} {{} t > \varepsilon}}}} \\ \end{aligned} \right. $$

δ 函数的强度，也称单位脉冲函数的冲量定义为 $S=\int_{-\infty}^{+\infty} \delta( t ) \mathrm{d} t=1$

$$L \big[ \delta( t ) \big]=1 $$

由于理论分析而已，是理想的函数

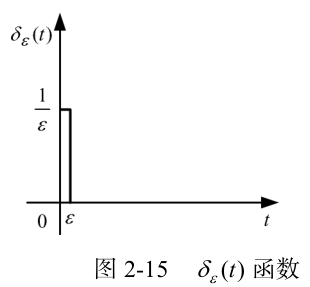
单位脉冲响应函数

卷积公式
$$y ( t )=L^{-1} [ Y ( s ) ]=L^{-1} [ G ( s ) R ( s ) ]=\int_{0}^{+\infty} g ( \tau) r ( t-\tau) \mathrm{d} \tau, ; ; ; t \geq0 $$

[!note]
线性定常系统的单位脉冲响应数值上等于改系统传递函数的反拉氏变换

U（s）=1 （t）

求解系统输出响应

输出求解为
$$y ( t )=L^{-1} \bigl[ Y ( s ) \bigr]=L^{-1} \bigl[ G ( s ) U ( s ) \bigr]=L^{-1} \bigl[ F ( s ) \bigr] $$
解法
- 结合留数进行求解最终大多是 exp（-xxt），位移性质
- 重根考虑求导加那个感叹号

典型环节及其传递函数

比例环节

输入输出成比例
$y ( t )=K u ( t )$
$$G ( s )={\frac{Y ( s )} {U ( s )}}=K $$
常见的比例环节实例有分压器、变压器、杠杆、线性放大器、无隙的传动齿轮组等

积分环节

输入的累积，表现为输出的变化速度和输入成正比
在单位阶跃输入激励下，积分环节的输出响应 Y（t）随时间直线上升

$$微分方程:y ( t )=K ! \int u ( t ) \mathrm{d} t $$

$$G ( s )={\frac{Y ( s )} {U ( s )}}={\frac{K} {s}}={\frac{1} {T s}} $$

惯性环节

物体对运动状态变化的阻抗程度

$$微分方程:T {\frac{\mathrm{d} y ( t )} {\mathrm{d} t}}+y ( t )=u ( t ) $$ $$G ( s )={\frac{Y ( s )} {U ( s )}}={\frac{1} {T s+1}} $$

单位阶跃响应$$Y ( s ) \!=\! G ( s ) U ( s ) \!=\! {\frac{1} {T s+1}} {\frac{1} {s}} \!=\! {\frac{1 / T} {s ( s \!+\! 1 / T )}} \!=\! {\frac{1} {s}} \!-\! {\frac{1} {s \!+\! 1 / T}} $$
跟随速度由 T 决定

振荡环节（二阶振荡环节）

$$T^{2} \, \frac{\mathrm{d}^{2} y ( t )} {\mathrm{d} t^{2}} \!+\! 2 \zeta T \frac{\mathrm{d} y ( t )} {\mathrm{d} t} \!+\! y ( t ) \!=\! u ( t ) $$

$$G ( s )=\frac{1} {T^{2} s^{2}+2 \zeta T s+1} $$
$T$ : 时间常数
$\zeta$ : 阻尼比 $0 < \zeta< 1$
$\omega_{n}$ : 自然振荡角频率